Toto je starší verze dokumentu!
Mathematics II
Due to coronavirus quarantine measures, the courses of Mathematics II will be held temporarily at distance, using electronic communication only.
Virus teaching regime:
- The primary communication channel is the email. We will contact you via your official email you have in KOS system. You may also use our email to contact us with anything related to our courses (asking questions, requesting extra study material, sending your completed homeworks).
- All the essential information and course materials will be published at this webpage. You will be notified of changes.
- A new, emergency communication channel for each course (subject) is set up at the university using Microsoft Teams platform. It can be used for online chat-like communication with teachers during the usual course hours according to standard schedule of the subject.
The Microsoft Team was created, for online consultations. Textbook material for implicit functions, Riemann, double and triple integral was added to the webpage.
General study advices and rules for the emergency online study regime can be found in Study advices
Essential weekly information for regular study
- Week: March 9 - March 15, 2020 - Topic: Implicit functions Implicit functions
- Week: March 16 - March 22, 2020 - Topic: Double integral Double integral
- Week: March 23 - March 30, 2020 - Topic: Triple integral Triple integral
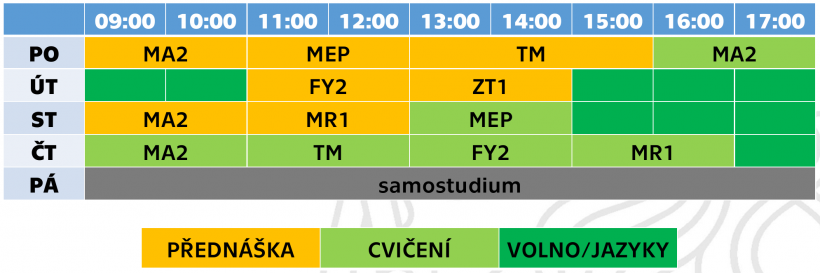
NEW Timetable (since March 23, 2020):
Yellow: Lectures, Green: Tutorials
For additional explanation, clarification and extra material contact the Lecture/Tutorial teacher by email or the Microsoft Team platform for online consultation. You can post your questions and request anytime. The teachers will respond as quickly as possible. For online live chat use the standard course hours according to usual schedule. Ask for other extra consultations if needed. We will do our best to help you.
This course is intended for foreign students studying at our faculty and domestic students who registered for this subject in their study plan. Conditions and requirements for this course are almost identical to the equivalent course being held in Czech language.
Content:
Functions of several variables - domain, limit, continuity, partial derivatives, extrema, implicit function. Multiple integrals - double and triple integral, Fubini's theorem, applications Line integral, surface integral, Gauss theorem, potential.
- Requirements - Level A(Alpha) in academic year 2019/2020
- Requirements - Level B(Beta) in academic year 2019/2020
Lecturers
doc. Mgr. Ing. Tomáš Bodnár, Ph.D., Office: KN:D-303
- lectures: Tuesday, 14:15 - 15:45 and Thursday 9:00 - 10:30.
Mgr. Hynek Řezníček , Office: KN:D-205b
- lectures: Wednesday 17:45-19:15 and Friday 9:00 - 10:30.
In the case of any problem (especially with assessments from tutorials, or with exams) contact your teacher.
Tutorials, assessments
Tutorials are obligatory. Assessment from tutorials (written in the study record) confirms student's presence and activity at the tutorials and elaboration of homework and tests. Assessment is a necessary condition for the exam. (I.e. student can make the exam only with the assessment written in the study record.) The assessments from tutorials obtained in previous years are not accepted. Student has to obtain the assessment again. The assessments are written in the last semestral week, not later than one week after. Exceptions are possible only with the explicit agreement of the chair of the institute.
Exams
The exams from Mathematics II (level A and B) will be organized in the same way as in Mathematics I. There are several necessary conditions to be fulfilled by students in order to be admitted to the exam:
- Student must have a valid assessment from tutorials registered in the electronic system KOS. (students without valid assessment can't subscribe for the exam)
- Student should come to the exam in time, i.e. he/she should be present in the examination room at least 10 minutes before the official start of the exam. (students who will come late, will be not allowed to participate in the exam)
- Student has to bring his/her Student Identification Card. (students will be not allowed to participate in the exam without presenting this card)
These conditions will be followed strictly, without any exceptions.
The detailed information will be made available at the end of semester in the Notice of exams from Mathematics II for the academic year 2019/20.
Literature:
- Neustupa, J., Kračmar S.: Mathematics II, CTU Publishing House, Prague, 1996,
- Finney, R. L., Thomas, G.B.: Calculus, Addison-Wesley, New York, Ontario, Sydney, 1994
Examples:
The Collection of examples from Mathematics II written in Czech by authors E. Brožíková, M. Kittlerová and F. Mráz (2016) contains both examples and their solutions. Here you find several parts translated in English. The examples in English have the same numbering but they are without solutions (corresponding solution you can find in the Czech version, which is in the brackets). English translations will be added gradually. By the star (*) are denoted the examples, which go beyond the requirements of the exam this year.
- Calculus - part 1 (partial derivatives, …) [Diferenciální počet-část 1]
- Calculus - part 2 (gradient, diferential, directional derivative, etc.) [Diferenciální počet-část 2]
- Divergence theorem [Gaussova-Ostrogradského věta]
Web additional sources:
- Keisler, H. J.: Elementary Calculus: An Infinitesimal Approach, 2nd edition, Prindle, Weber & Schmidt, 1986.
- Paul's Online Math Notes have gotten the notes/tutorials for Algebra, Calculus I, Calculus II, Calculus III and Differential Equations class online.
- Just Math Tutoring is a web site of Patrick from Vanderbilt University, who provide clear and thorough explanations, and to present them in an environment in which the student is comfortable.
- The Math Insight web site is a collection of pages and applets designed to shed light on concepts underlying a few topics in mathematics (see Index)
- Mathispoewr4u tutorials. This site provides over 3,500 free mini-lessons and example videos with no ads. The videos are organized by course and topic.


